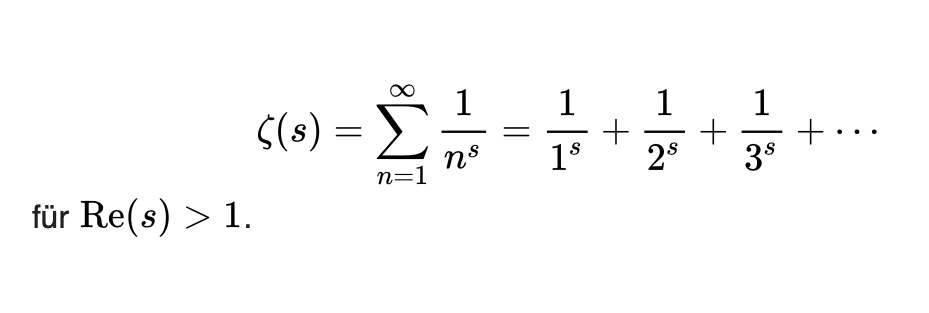Das Verhalten der Riemannschen Zeta-Funktion in den Bereichen


gilt als gut verstanden. Jedoch sind ihre Eigenschaften innerhalb des kritischen Streifens

weitestgehend unbekannt und Gegenstand bedeutender Vermutungen.
Dies betrifft unter anderem die Fragen nach asymptotischem Wachstum in imaginärer Richtung und der für die Zahlentheorie so wichtigen Nullstellenverteilung.
Nach heutigem Wissensstand beschreibt die Zeta-Funktion im Streifen

im Wesentlichen Chaos.
Die Werte der Nullstellen bauen nicht nur Brücken zur Theorie der Primzahlen, sondern höchstwahrscheinlich auch zur modernen Quantenphysik.
Die Nullstellen der Zeta-Funktion erzeugen einen Korrekturterm, der sie in einen exakten Ausdruck umwandelt. Diese dadurch entstehende exakte Formel kennt also die Verteilung der Primzahlen bis ins letzte Detail. Damit gelten die Fragen um die Primzahlen jedoch nicht als gelöst: der Rechenaufwand nimmt mit steigenden Werten sehr stark zu, somit sind praktische Berechnungen mit dieser Formel nicht effektiv. Für numerische Forschung eignen sich im Gegensatz dazu moderne Primzahltests besser. Die exakte Formel ist jedoch von theoretischem Interesse: Sie birgt nämlich den Fehlerabstand zwischen der einfachen Vorhersage und der tatsächlichen Primzahlverteilung. Es wird vermutet, dass dieser Fehler (innerhalb des Spektrums aller Möglichkeiten) kleinstmöglich ist. Dabei wäre eine Entschlüsselung dieses Fehlers nicht so sehr für die Numerik von Relevanz. Vielmehr ist die reine Mathematik bestrebt, den bisher verborgenen Grund zu erfahren, weshalb der Fehler (falls zutreffend) so klein wie möglich ausfällt.